Здесь мы рассмотрим разложения в ряды более широкого класса функций, чем рассматривали прежде, а именно: будем изучать такие (однозначные) функции, которые аналогичны не во всем круге z - zo z - zq г = 0, т.е. разложение функции в проколотой окрестности точки zq. Эти разложения позволяют изучать функции в окрестности точек, где они теряют аналитичность (особых точек).
Заметим, что степенных рядов нам теперь будет недостаточно, поскольку такими рядами представляются только функции, аналитические во всем круге z - zq (см. теорему 22.1). Но мы добавим к членам c n (z - zo) n с неотрицательными значениями п соответствующие члены с п = -1, -2,... и рассмотрим сумму двух рядов
Разложение функции f(z) в кольце будем искать в виде
причем под сходимостью ряда c n (z - zq)" понимается сходи-
мость обоих рядов в правой части (25.1). Как и в §22, мы докажем теоремы о существовании и единственности такого разложения. Начнем с теоремы существования.
Теорема 25.1 (теорема Лорана). Пусть функция f(z) аполитична а кольце V = {г z - zo:
коэффициенты которого определяются по формулой
(здесь р - произвольное число, заключенное между г и R).

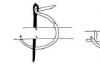
Доказательство. Пусть z - какая-либо точка кольца V. Построим кольцо V = {г" C, - zq R"}, лежащее внутри кольца V и содержащее точку z. Для этого следует выбрать числа г" и R 1 так, чтобы г R" (рис. 47).
Обозначим через Г и Г> окружности 1C - zo = R" и |С - Zo = г"; обход обеих окружностей зададим против часовой стрелки. Через TV обозначим окружность |С - za = г" с обходом по часовой стрелке. Функция f(z) аналитична в замкнутой области V 7 , граница Г 7 которой состоит из кривых Гх и 17 (напомним, что при обходе границы область должна оставаться слева). По интегральной формуле Коши (см. теорему 18.1)
Разложение в ряд первого интеграла в правой части (25.4) проводится так же, как и в доказательстве теоремы 22.2. Функцию представляем в виде

причем ряд (25.5) сходится абсолютно и равномерно по переменному
С на IV Умножая равенства (25.5) на функцию ^-:/(?), ограничениям
ную на Г1 (согласно замечанию 20.5, равномерная сходимость рядов в (25.5) при этом нс нарушается), и почленно интегрируя вдоль IV получаем

Итак, первый интеграл в правой части (25.4) мы разложили в сходящийся ряд по степеням (z - г«). Второй интеграл в (25.4) придется разлагать иначе, поскольку для С € Гг будет z - zo > |С - Zq и, следовательно, ряды в (25.5) расходятся. Имеем
Снова применяя формулу (22.С), получаем
При всех С € Г2 выполняются равенства
Поскольку ряд qi n сходится, то в силу признака равномерной
сходимости Вейерштрасса (теорема 20.2) ряд в правой части (25.8) сходится на Г о абсолютно и равномерно по переменному?. Нам удобно переписать этот ряд в несколько иной форме, введя новый индекс суммирования к равенством к = -п - 1, т.е. п = -к - 1. Когда п принимает значения 0,1,2,..., индекс к пробегает значения -1, -2, -3____
Умножим равенства (25.9) на f(Q (что не нарушит равномерной
сходимости рядов в (25.9) на окружности Гг) и почленно проинтегрируем вдоль Гг:

Индекс к в формулах (25.10), (25.11) можно заменить любой другой буквой; в частности, можно снова обозначить его через н, где п = - 1,- 2,... Подставляя разложения (25.6) и (25.10) в (25.4), придем к равенству (25.2). Функция . является аналитической
(С - zo) n + l
в кольце г г 0 р, такое что г то обе окружности Ti и Гг можно заменить окружностью |С - zq = р. При этом равенства (25.7) и (25.11) запишутся единой формулой (25.3). Теорема 25.3 доказана.
Ряд (25.2) по целым степеням (z - -го) (как положительным, так и отрицательным), коэффициенты которого определяются но форму-
лам (25.3), называется рядом Лорана функции f(z). Ряд ^2 c n (z -
п =0
- - Zo) n называется правильной частью , а ряд c n (z - zq) u (пишут
также c n{ z - z o) n) - главной частью ряда Лорана (обоснован-
ность названий выяснится в дальнейшем).
Перейдем теперь к вопросу о единственности разложения (25.2).
Теорема 25.2 (теорема единственности разложения функции в ряд Лорана). Пусть в некотором, кольце V = {г z - zo (25.2). Тогда f(z ) является
аналитической в V функцией, а коэффициенты с п, п = 0, ±1, ±2.... разложения определяются однозначно по формулам, (25.3).
Доказательство. Так как по условию теоремы ряд (25.2) сходится в V, то сходятся оба ряда в правой части (25.1), состав-
ляющие ряд (25.2). Первый из них - ряд Y1 °n(z ~ z o) n ~ является
обычным степенным рядом, сходящимся в некотором круге с центром Zo и расходящимся вне этого круга. Поскольку этот ряд сходится в V , то все кольцо V лежит в круге сходимости. Так как сумма
степенного ряда аналитична в круге сходимости (свойство 21.6), то
сумма Si (.г) ряда c n (z - zq) h аналитична в V. По свойству 21.5,
этот ряд равномерно сходится в любом круге z - zq R"
но ряд c n{z - zo) n - Сделаем замену переменных, положив Z =
=-, к = - п. Тогда изучаемый ряд примет вид V C-uZ k . Этот
z ~ z o k=l
ряд является степенным рядом относительно переменного Z с центром Zo = 0: он сходится в некотором круге с R"o этот ряд сходится равномерно (свойство 21.5). Возвратимся теперь к переменному z. Тогда круг
/?о перейдет в множество --- z - zo > 1 /Ro, т.е. во внешность круга с центром zq радиуса 1/Ло- Таким образом, ряд
^2 c n (z - Zo) n сходится при |z - Zo > l/Ro к аналитической функ- п =-1
ции 5-2(г) и расходится при z - zo 1 /Rq. Поскольку этот ряд сходится в V, то все кольцо V лежит в области сходимости z - Zo > 1/Яо этого ряда. При этом в области z - zo > 1 //?о с Н® Но сходимость будет равномерной. В частности, рад равномерно сходится при |z - zo > г ", если г" > г.
Итак, оба ряда в правой части (25.1) сходятся в кольце V и их суммы Si (г) и S-j(z) аналитичны в V. Значит, функция f(z) = Si (z) + 4* S-z(z) аналитична в V .
Покажем, что коэффициенты с п разложения определяются однозначно по формулам (25.3). Возьмем окружность Г = {z - zo = /?}, где г Подберем числа г" и R" так, чтобы г Оба ряда в правой части (25.1) равномерно сходятся в кольце V = = {г; z - Zo R 1 }- Значит, и ряд

сходится в нем равномерно. Это свойство сохранится после умножения обеих частей на произвольную степень (z - zo)~ n ~ l , n = О, ±1, ±2_____ так как каждая из этих степеней является функцией, ограни
ченной в V (см. замечание 20.5):
В силу теоремы 20.4 полученный ряд можно почленно интегрировать вдоль Г:
Воспользуемся теперь равенством (15.7):
согласно которому все интегралы в левой части (25.12) равны нулю, кроме одного, для которого к - п - 1 = - 1 (т.е. к = гг) и который равен 2тгг. Поэтому в сумме из (25.12) остается лишь одно слагаемое при к = п, и мы получаем
что равносильно равенствам (25.3). Теорема 25.2 доказана.
При доказательстве теоремы 25.2 мы установили, что ряд (25.2) сводится к объединению двух степенных рядов, один из которых сходится внутри некоторот круга с центром zq, а другой - вне круга меньшего радиуса с гем же центром (если бы радиус второго круга был больше, то множество сходимости ряда (25.2) было бы пустым). Обозначим радиусы этих кругов R и г соответственно (здесь не утверждается, ч то эти числа совпадают с внешним и внутренним радиусами кольца V в теоремах 25.1, 25.2). Отсюда и из свойств степенных рядов (см. §21) вытекают следующие свойства ряда (25.2).
Свойство 25.3. Множеством сходимости ряда (25.2) является кольцо V = {г z - zq R) с возможным добавлением некоторых или всех точек на его границе. При этом возможны случаи г = 0 и R = оо.
Свойство 25.4. Сумма 5(г) ряда (25.2) является аналитической функцией внутри кольца V .
Свойство 25.5. Ряд (25.2) можно почленно интегрировать и почленно дифференцировать внутри кольца V любое число jhm. Полученные при этом ряды имеют то же кольцо сходимости V , что
и исходный ряд (25.2); сходимость в граничных точках может не сохраняться.
Свойство 25.6. Если V = {г Zo является кольцом сходимости ряда Лорана функции f(z ) и 0
Доказательство. Ряд Лорана функции /(z) есть объединено оо 1
ние двух степенных рядов °n(z ~ z o) n и c_*Z*, где Z =-.
n=0 k- z - Z 0
Кругами СХОДИМОСТИ ЭТИХ рядов ЯВЛЯЮТСЯ z - 2о| R и z - zo = R и = 1/г (т.е. z - zo = г) лежат особые точки
функций Si(z) = c n{z - Zq) u и S- 2 (z) = Cn(z-z 0) n соответ-
ственно. Следовательно, на этих окружностях лежат особые точки функции f(z) = Si (г) + S- 2 (z), что и требовалось доказать.
Дчя нахождения разложений в ряд Лорана широко используются те же приемы, что и для разложения в ряд Тейлора, а именно метод подстановки, почленное интегрирование и дифференцирование рядов и т.д.
П р и м е р 25.7. Найти все лорановские разложения функции
/( г) = f по степеням (z - 1).
" z(z - 1)
Решение. Сделаем замену переменного: w = z - 1, т.е. z = w +
1. Выполнив подстановку, получим функцию г/(гс) = . w . . Раз-
{w + 1)wj
ложим полученную дробь в сумму пр(хдейших дробей (подробнее о разложении в сумму простейших дробей см. §32). Разложение будем искать в виде

где А и D числа, которые пред сшит найти. С этой целью приведем дроби, стоящие справа, к общему знаменателю:

Отсюда следует, что w + 2 = A(w + 1) + Bw, причем равенство выполнено при всех значениях w , включая w = 0 и w = - 1 (это следует из непрерывности левой и правой частей этого равенства). При w = 0 получаем 2 = .4, т.е. А = 2; подставляя w = -1, имеем 1 = -В, т.е. В = - 1. Таким образом,

Эта функция имеет особые точки w = 0, w = - 1 и, следовательно, аполитична в кольцах V’i = {0 w
При w > 1 полученный ряд перестает сходиться. Поэтому для разложения функции g(w) в кольце У 2 следует преобразовать дробь:

При |ш| > 1 будет -
вместо z подставить в нее l/w. Выполняя указанные подстановки, получим

(мы сделали замену к = - (п + 1) и воспользовались равенством (- 1)* = (-I) - *). Возвращаясь к переменному z - w + 1, получаем искомые разложения функции f(z):

ного члена -- (все остальные коэффициенты главной части рав
ны нулю), а ряд в (25.13) дает правильную часть разложения. При 1 z - 1| z - 1| = 0 с радиусом 0и|г-1| = 1с радиусом 1) содержат особые точки функции f(z).
Как вставить математические формулы на сайт?
Если нужно когда-никогда добавлять одну-две математические формулы на веб-страницу, то проще всего сделать это, как описано в статье : математические формулы легко вставляются на сайт в виде картинок, которые автоматически генерирует Вольфрам Альфа. Кроме простоты, этот универсальный способ поможет улучшить видимость сайта в поисковых системах. Он работает давно (и, думаю, будет работать вечно), но морально уже устарел.
Если же вы постоянно используете математические формулы на своем сайте, то я рекомендую вам использовать MathJax - специальную библиотеку JavaScript, которая отображает математические обозначения в веб-браузерах с использованием разметки MathML, LaTeX или ASCIIMathML.
Есть два способа, как начать использовать MathJax: (1) при помощи простого кода можно быстро подключить к вашему сайту скрипт MathJax, который будет в нужный момент автоматически подгружаться с удаленного сервера (список серверов ); (2) закачать скрипт MathJax с удаленного сервера на свой сервер и подключить ко всем страницам своего сайта. Второй способ - более более сложный и долгий - позволит ускорить загрузку страниц вашего сайта, и если родительский сервер MathJax по каким-то причинам станет временно недоступен, это никак не повлияет на ваш собственный сайт. Несмотря на эти преимущества, я выбрал первый способ, как более простой, быстрый и не требующий технических навыков. Следуйте моему примеру, и уже через 5 минут вы сможете использовать все возможности MathJax на своем сайте.
Подключить скрипт библиотеки MathJax с удаленного сервера можно при помощи двух вариантов кода, взятого на главном сайте MathJax или же на странице документации :
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.
Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Любой фрактал строится по определенному правилу, которое последовательно применяется неограниченное количество раз. Каждый такой раз называется итерацией.
Итеративный алгоритм построения губки Менгера достаточно простой: исходный куб со стороной 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из него удаляются один центральный куб и 6 прилежащих к нему по граням кубов. Получается множество, состоящее из 20 оставшихся меньших кубов. Поступая так же с каждым из этих кубов, получим множество, состоящее уже из 400 меньших кубов. Продолжая этот процесс бесконечно, получим губку Менгера.
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
,
где r n
– так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
![]() , где число x заключено между х и а.
, где число x заключено между х и а.
f(x)=
в точке x 0 = Количество элементов ряда 3 4 5 6 7
Использовать разложение элементарных функций e x , cos(x), sin(x), ln(1+x), (1+x) m
Правила ввода функций :
Если для некоторого значения х
r n
→0 при n
→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора
:
,
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
1) она имеет производные всех порядков;
2) построенный ряд сходится в этой точке.
При а =0 получаем ряд, называемый рядом Маклорена
:
,
Разложение простейших (элементарных) функций в ряд Маклорена:
Показательные функции
, R=∞
Тригонометрические функции
![]() , R=∞
, R=∞
![]() , R=∞
, R=∞
, (-π/2 < x < π/2), R=π/2
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции
Логарифмические функции
, -1